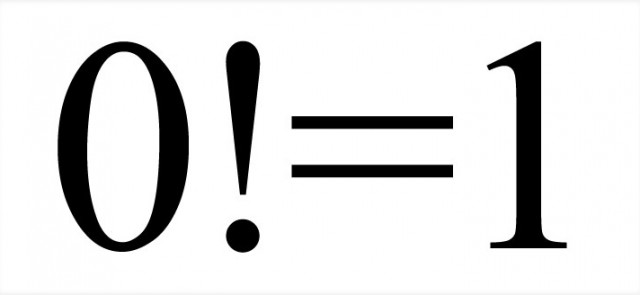How Many Triangles ??

Answer : 27

Read more →

Can You Answer This..??

Options:

A.18

B.24

C.16

D:None

Read more →

Voltage Transformer Basics

One of the main reasons that we use alternating AC voltages and currents in our homes and workplace’s is that AC supplies can be easily generated at a convenient voltage, transformed (hence the name transformer) into much higher voltages and then distributed around the country using a national grid of pylons and cables over very long distances.

The reason for transforming the voltage to a much higher level is that higher distribution voltages implies lower currents for the same power and therefore lower I²R losses along the networked grid of cables. These higher AC transmission voltages and currents can then be reduced to a much lower, safer and usable voltage level where it can be used to supply electrical equipment in our homes and workplaces, and all this is possible thanks to the basic Voltage Transformer.

A Typical Voltage Transformer

The Voltage Transformer can be thought of as an electrical component rather than an electronic component. A transformer basically is very simple static (or stationary) electro-magnetic passive electrical device that works on the principle of Faraday’s law of induction by converting electrical energy from one value to another.

The transformer does this by linking together two or more electrical circuits using a common oscillating magnetic circuit which is produced by the transformer itself. A transformer operates on the principals of “electromagnetic induction”, in the form of  Mutual Induction.

Mutual induction is the process by which a coil of wire magnetically induces a voltage into another coil located in close proximity to it. Then we can say that transformers work in the “magnetic domain”, and transformers get their name from the fact that they “transform” one voltage or current level into another.

Transformers are capable of either increasing or decreasing the voltage and current levels of their supply, without modifying its frequency, or the amount of Electrical Power being transferred from one winding to another via the magnetic circuit.

A single phase voltage transformer basically consists of two electrical coils of wire, one called the “Primary Winding” and another called the “Secondary Winding”. For this tutorial we will define the “primary” side of the transformer as the side that usually takes power, and the “secondary” as the side that usually delivers power. In a single-phase voltage transformer the primary is usually the side with the higher voltage.

These two coils are not in electrical contact with each other but are instead wrapped together around a common closed magnetic iron circuit called the “core”. This soft iron core is not solid but made up of individual laminations connected together to help reduce the core’s losses.

The two coil windings are electrically isolated from each other but are magnetically linked through the common core allowing electrical power to be transferred from one coil to the other. When an electric current passed through the primary winding, a magnetic field is developed which induces a voltage into the secondary winding as shown.

Single Phase Voltage Transformer

In other words, for a transformer there is no direct electrical connection between the two coil windings, thereby giving it the name also of an Isolation Transformer. Generally, the primary winding of a transformer is connected to the input voltage supply and converts or transforms the electrical power into a magnetic field. While the job of the secondary winding is to convert this alternating magnetic field into electrical power producing the required output voltage as shown.

Transformer Construction (single-phase)

• Where:
•   V_P  -  is the Primary Voltage
•   V_S  -  is the Secondary Voltage
•   N_P  -  is the Number of Primary Windings
•   N_S  -  is the Number of Secondary Windings
•   Φ (phi)  -  is the Flux Linkage

Notice that the two coil windings are not electrically connected but are only linked magnetically. A single-phase transformer can operate to either increase or decrease the voltage applied to the primary winding. When a transformer is used to “increase” the voltage on its secondary winding with respect to the primary, it is called a Step-up transformer. When it is used to “decrease” the voltage on the secondary winding with respect to the primary it is called a Step-down transformer.

However, a third condition exists in which a transformer produces the same voltage on its secondary as is applied to its primary winding. In other words, its output is identical with respect to voltage, current and power transferred. This type of transformer is called an “Impedance Transformer” and is mainly used for impedance matching or the isolation of adjoining electrical circuits.

The difference in voltage between the primary and the secondary windings is achieved by changing the number of coil turns in the primary winding ( N_P ) compared to the number of coil turns on the secondary winding ( N_S ).

As the transformer is basically a linear device, a ratio now exists between the number of turns of the primary coil divided by the number of turns of the secondary coil. This ratio, called the ratio of transformation, more commonly known as a transformers “turns ratio”, ( TR ). This turns ratio value dictates the operation of the transformer and the corresponding voltage available on the secondary winding.

It is necessary to know the ratio of the number of turns of wire on the primary winding compared to the secondary winding. The turns ratio, which has no units, compares the two windings in order and is written with a colon, such as 3:1 (3-to-1). This means in this example, that if there are 3 volts on the primary winding there will be 1 volt on the secondary winding, 3 volts-to-1 volt. Then we can see that if the ratio between the number of turns changes the resulting voltages must also change by the same ratio, and this is true.

Transformers are all about “ratios”. The ratio of the primary to the secondary, the ratio of the input to the output, and the turns ratio of any given transformer will be the same as its voltage ratio. In other words for a transformer: “turns ratio = voltage ratio”. The actual number of turns of wire on any winding is generally not important, just the turns ratio and this relationship is given as:

A Transformers Turns Ratio

Assuming an ideal transformer and the phase angles:  Φ_P ≡ Φ_S

Note that the order of the numbers when expressing a transformers turns ratio value is very important as the turns ratio 3:1 expresses a very different transformer relationship and output voltage than one in which the turns ratio is given as: 1:3.

Transformer Basics Example No1

A voltage transformer has 1500 turns of wire on its primary coil and 500 turns of wire for its secondary coil. What will be the turns ratio (TR) of the transformer.

 

This ratio of 3:1 (3-to-1) simply means that there are three primary windings for every one secondary winding. As the ratio moves from a larger number on the left to a smaller number on the right, the primary voltage is therefore stepped down in value as shown.

Transformer Basics Example No2

If 240 volts rms is applied to the primary winding of the same transformer above, what will be the resulting secondary no load voltage.

 

Again confirming that the transformer is a “step-down transformer as the primary voltage is 240 volts and the corresponding secondary voltage is lower at 80 volts.

Then the main purpose of a transformer is to transform voltages at preset ratios and we can see that the primary winding has a set amount or number of windings (coils of wire) on it to suit the input voltage. If the secondary output voltage is to be the same value as the input voltage on the primary winding, then the same number of coil turns must be wound onto the secondary core as there are on the primary core giving an even turns ratio of 1:1 (1-to-1). In other words, one coil turn on the secondary to one coil turn on the primary.

If the output secondary voltage is to be greater or higher than the input voltage, (step-up transformer) then there must be more turns on the secondary giving a turns ratio of 1:N (1-to-N), where N represents the turns ratio number. Likewise, if it is required that the secondary voltage is to be lower or less than the primary, (step-down transformer) then the number of secondary windings must be less giving a turns ratio of N:1 (N-to-1).

Transformer Action

We have seen that the number of coil turns on the secondary winding compared to the primary winding, the turns ratio, affects the amount of voltage available from the secondary coil. But if the two windings are electrically isolated from each other, how is this secondary voltage produced?

We have said previously that a transformer basically consists of two coils wound around a common soft iron core. When an alternating voltage ( V_P ) is applied to the primary coil, current flows through the coil which in turn sets up a magnetic field around itself, called mutual inductance, by this current flow according to Faraday’s Law of electromagnetic induction. The strength of the magnetic field builds up as the current flow rises from zero to its maximum value which is given as dΦ/dt.

As the magnetic lines of force setup by this electromagnet expand outward from the coil the soft iron core forms a path for and concentrates the magnetic flux. This magnetic flux links the turns of both windings as it increases and decreases in opposite directions under the influence of the AC supply.

However, the strength of the magnetic field induced into the soft iron core depends upon the amount of current and the number of turns in the winding. When current is reduced, the magnetic field strength reduces.

When the magnetic lines of flux flow around the core, they pass through the turns of the secondary winding, causing a voltage to be induced into the secondary coil. The amount of voltage induced will be determined by: N.dΦ/dt (Faraday’s Law), where N is the number of coil turns. Also this induced voltage has the same frequency as the primary winding voltage.

Then we can see that the same voltage is induced in each coil turn of both windings because the same magnetic flux links the turns of both the windings together. As a result, the total induced voltage in each winding is directly proportional to the number of turns in that winding. However, the peak amplitude of the output voltage available on the secondary winding will be reduced if the magnetic losses of the core are high.

If we want the primary coil to produce a stronger magnetic field to overcome the cores magnetic losses, we can either send a larger current through the coil, or keep the same current flowing, and instead increase the number of coil turns ( N_P ) of the winding. The product of amperes times turns is called the “ampere-turns”, which determines the magnetising force of the coil.

So assuming we have a transformer with a single turn in the primary, and only one turn in the secondary. If one volt is applied to the one turn of the primary coil, assuming no losses, enough current must flow and enough magnetic flux generated to induce one volt in the single turn of the secondary. That is, each winding supports the same number of volts per turn.

As the magnetic flux varies sinusoidally, Φ = Φ_max sinωt, then the basic relationship between induced emf, ( E ) in a coil winding of N turns is given by:

emf = turns x rate of change

• Where:
•   ƒ  -  is the flux frequency in Hertz,  = ω/2π
•   Ν  -  is the number of coil windings.
•   Φ  -  is the flux density in webers

This is known as the Transformer EMF Equation. For the primary winding emf, N will be the number of primary turns, ( N_P ) and for the secondary winding emf, N will be the number of secondary turns, ( N_S ).

Also please note that as transformers require an alternating magnetic flux to operate correctly, transformers cannot therefore be used to transform or supply DC voltages or currents, since the magnetic field must be changing to induce a voltage in the secondary winding. In other words, Transformers DO NOT Operate on DC Voltages, ONLY AC.

If a transformers primary winding was connected to a DC supply, the inductive reactance of the winding would be zero as DC has no frequency, so the effective impedance of the winding will therefore be very low and equal only to the resistance of the copper used. Thus the winding will draw a very high current from the DC supply causing it to overheat and eventually burn out, because as we know I = V/R.

Transformer Basics Example No3

A single phase transformer has 480 turns on the primary winding and 90 turns on the secondary winding. The maximum value of the magnetic flux density is 1.1T when 2200 volts, 50Hz is applied to the transformer primary winding. Calculate:

a). The maximum flux in the core.

 

b). The cross-sectional area of the core.

 

c). The secondary induced emf.

Electrical Power in a Transformer

Another one of the transformer basics parameters is its power rating. Transformers are rated in Volt-amperes, ( VA ), or in larger units of Kilo Volt-amperes, ( kVA ). In an ideal transformer (ignoring any losses), the power available in the secondary winding will be the same as the power in the primary winding, they are constant wattage devices and do not change the power only the voltage to current ratio. Thus, in an ideal transformer the Power Ratio is equal to one (unity) as the voltage, V multiplied by the current, I will remain constant.

That is the electric power at one voltage/current level on the primary is “transformed” into electric power, at the same frequency, to the same voltage/current level on the secondary side. Although the transformer can step-up (or step-down) voltage, it cannot step-up power. Thus, when a transformer steps-up a voltage, it steps-down the current and vice-versa, so that the output power is always at the same value as the input power. Then we can say that primary power equals secondary power, ( P_P = P_S ).

Power in a Transformer

 

Where: Φ_P is the primary phase angle and Φ_S is the secondary phase angle.

Note that since power loss is proportional to the square of the current being transmitted, that is: I²R, increasing the voltage, let’s say doubling ( ×2 ) the voltage would decrease the current by the same amount, ( ÷2 ) while delivering the same amount of power to the load and therefore reducing losses by factor of 4. If the voltage was increased by a factor of 10, the current would decrease by the same factor reducing overall losses by factor of 100.

Transformer Basics – Efficiency

A transformer does not require any moving parts to transfer energy. This means that there are no friction or windage losses associated with other electrical machines. However, transformers do suffer from other types of losses called “copper losses” and “iron losses” but generally these are quite small.

Copper losses, also known as I²R loss is the electrical power which is lost in heat as a result of circulating the currents around the transformers copper windings, hence the name. Copper losses represents the greatest loss in the operation of a transformer. The actual watts of power lost can be determined (in each winding) by squaring the amperes and multiplying by the resistance in ohms of the winding (I²R).

Iron losses, also known as hysteresis is the lagging of the magnetic molecules within the core, in response to the alternating magnetic flux. This lagging (or out-of-phase) condition is due to the fact that it requires power to reverse magnetic molecules; they do not reverse until the flux has attained sufficient force to reverse them.

Their reversal results in friction, and friction produces heat in the core which is a form of power loss. Hysteresis within the transformer can be reduced by making the core from special steel alloys.

The intensity of power loss in a transformer determines its efficiency. The efficiency of a transformer is reflected in power (wattage) loss between the primary (input) and secondary (output) windings. Then the resulting efficiency of a transformer is equal to the ratio of the power output of the secondary winding, P_S to the power input of the primary winding, P_P and is therefore high.

An ideal transformer is 100% efficient because it delivers all the energy it receives. Real transformers on the other hand are not 100% efficient and at full load, the efficiency of a transformer is between 94% to 96% which is quiet good. For a transformer operating with a constant voltage and frequency with a very high capacity, the efficiency may be as high as 98%. The efficiency, η of a transformer is given as:

Transformer Efficiency

where: Input, Output and Losses are all expressed in units of power.

Generally when dealing with transformers, the primary watts are called “volt-amps”, VA to differentiate them from the secondary watts. Then the efficiency equation above can be modified to:

 

It is sometimes easier to remember the relationship between the transformers input, output and efficiency by using pictures. Here the three quantities of VA, W and η have been superimposed into a triangle giving power in watts at the top with volt-amps and efficiency at the bottom. This arrangement represents the actual position of each quantity in the efficiency formulas.

Transformer Efficiency Triangle

 

and transposing the above triangle quantities gives us the following combinations of the same equation:

 

Then, to find Watts (output) = VA x eff., or to find VA (input) = W/eff., or to find Efficiency, eff. = W/VA, etc.

Transformer Basics Summary

Then to summarise this transformer basics tutorial. A Transformer changes the voltage level (or current level) on its input winding to another value on its output winding using a magnetic field. A transformer consists of two electrically isolated coils and operates on Faraday’s principal of “mutual induction”, in which an EMF is induced in the transformers secondary coil by the magnetic flux generated by the voltages and currents flowing in the primary coil winding.

Both the primary and secondary coil windings are wrapped around a common soft iron core made of individual laminations to reduce eddy current and power losses. The primary winding of the transformer is connected to the AC power source which must be sinusoidal in nature, while the secondary winding supplies power to the load.

We can represent the transformer in block diagram form as follows:

Basic Representation of the Transformer

 

The ratio of the transformers primary and secondary windings with respect to each other produces either a step-up voltage transformer or a step-down voltage transformer with the ratio between the number of primary turns to the number of secondary turns being called the “turns ratio” or “transformer ratio”.

If this ratio is less than unity, n < 1 then N_S is greater than N_P and the transformer is classed as a step-up transformer. If this ratio is greater than unity, n > 1, that is N_P is greater than N_S, the transformer is classed as a step-down transformer. Note that single phase step-down transformer can also be used as a step-up transformer simply by reversing its connections and making the low voltage winding its primary, and vice versa as long as the transformer is operated within its original VA design rating.

If the turns ratio is equal to unity, n = 1 then both the primary and secondary have the same number of windings, therefore the voltages and currents are the same for both windings.

This type of transformer is classed as an isolation transformer as both the primary and secondary windings of the transformer have the same number of volts per turn. The efficiency of a transformer is the ratio of the power it delivers to the load to the power it absorbs from the supply. In an ideal transformer there are no losses so no loss of power then Pin = Pout.

In the next tutorial to do with Transformer Basics, we will look at the physical Construction of a Transformer and see the different magnetic core types and laminations used to support the primary and secondary windings.

Read more →

What is the use of integration and differentiation?

What is the use of integration and differentiation?

Let us get into this with all interest. Yes integration is a reverse process of differentiation.
First let us put the question why do we need such a mathematical process called integration. Actually integration is nothing but the summing up of a lot, some million and million items.
Let me explain how.
Suppose you want to find the volume of a cone of radius r and height h.
Let the cone be seated such that its vertex get coincided with the origin and its height be along the x -axis.
In case of a cylinder the radius will be the same at all heights and so if you consider a small part both the sides of that part will have the same radius and so no problem in finding the volume.
But in the case of the cone, as we move away from the origin along x-axis the radius of the cone will be gradually increasing.
So as you consider a slice any where in the cone both the sides of the slice will not definitely have same radius. Is that ok?
Now calculus comes into play.
You choose a small slice in such a way that both the sides of the slice would have almost the same radius. It is possible only when you have a slice of negligible thickness. Such negligible thickness is denoted mathematically denoted as dx which means delta x tending to zero.
Once again note down the statement: delta x tending to zero. This means delta x is very so near to zero but not zero.
With such....... thickness, both sides of the slice would have the same radius.Let the slice of thickness dx be chosen at a distance x from the origin and let the radius of the slice be y at that position. Then the volume of our slice will be pi y^2 dx. Now imagine! Such slices, innumerable in number, can be got in the cone right moving from the origin and extending upto the total length (height) h of the cone. So we must collect all such slices and add their volumes to get the actual or total volume of the cone.
So we integrate the term pi y^2 dx within the limits of x ie 0 to h.
Now it becomes more essential to replace y interms of x. How can we do this? By using similar triangle concept, the ratio of the corresponding sides will be the same. So y/x = r/h
From this we can easily have y as (r/h) x.
Now replacing y we get the expression to be integrated (usually named as integrand) as pi (r/h)^2 x^2 dx. The formula for integral of x^n dx is given as x^(n+1) /(n+1).
So following this we get the integral value as pi(r/h)^2 (x^3 /3).
Next important step is supplying limit of x.
First upper limit h. This would give a value of pi(r/h)^2 (h^3 /3)
With lower limit 0, the value would become 0
Now the difference between these two values will be the required volume of the cone.
That comes to be 1/3 pi r^2 h. (cancelling h^2)
So interesting! See how much helpful the technique of integration in finding the volume of the cone!
By differentiation, we chop things into finer and by integration we collect all such finer.
Hope you have got a gist of the tremendous usage of the branch of mathematics, named as calculus.

Read more →

Is the number 0 even or odd..?

Is the number 0 even or odd..? 

 

A number is even if it is divisible by 2 without a remainder. For Example 8 is even since 8 divided by 2 is 4, and 12 is even since 12 divided by 2 is 6, but 7 is not even since 7 divided by 2 is 3 with a remainder of 1. 

What about zero? Zero divided by 2 is zero with no remainder so zero is even. 

Read more →

Why 0! is equal to 1 ..??

Why 0! is equal to 1 ..??

We Know ,

n! = n x (n-1)!

Dividing both sides by n , We get

n!/n = n x (n-1)!/n 

Or, n!/n = (n-1)!

Or, (n-1)! = n!/n

Now , Putting n=1 , We get

(1-1)! = 1!/1

i.e. 0! = 1 

  

Read more →

Funniest Math/Science Questions and answers

Q. How can you drop a raw egg onto a concrete floor without cracking it?

A. Concrete floors are very hard to crack!



Q. If it took eight men ten hours to build a wall, how long would it take
four men to build it?

A. No time at all it is already built.



Q. If you had three apples and four oranges in one hand and four apples
and three oranges in the other hand, what would you have?

A. Very large hands. (Good one)



Q. How can you lift an elephant with one hand?

A. It is not a problem, since you will never find an elephant with
one hand.




Q. How can a man go eight days without sleep?

A. No Probs , He sleeps at night.



Q. If you throw a red stone into the blue sea what it will become?

A. It will Wet or Sink as simple as that.



Q. What looks like half apple ?

A: The other half.



Q. What can you never eat for breakfast ?

A: Dinner.



Q. What happened when wheel was invented ?

A: It caused a revolution.



Q. Bay of Bengal is in which state?

A: Liquid

Read more →

Math Puzzle Questions

1. What is come in place of question mark (?) in the following series?





(a) HS

(b) IT

(c) IS

(d) HT



Solution:

2. If A is substituted by 4, B by 3, C by 2, D by 4, E by 3, F by 2 and so on, then what will be total of the numerical values of the letters of the word SICK?

(a) 11

(b) 12

(c) 10

(d) 9



Solution:

Total value = 4 + 2 + 2 + 3 = 11.

Answer: (a)



3. Four of the following five are alike in a certain way and hence form a group. Which one does not belong to the group?

(a) 52

(b) 70

(c) 48

(d) 68



Solution:All the numbers are multiple of 4, except 70.

Answer: (b)



4. If U is denoted by 7, M by 2, I by 5, O by 1, K by 8 and J by 4, then what will be the numeric form of the word MOUJIK when written in the reverse order?

(a) 217458

(b) 845712

(c) 854712

(d) 857412



Solution:

217458 is the number.

Now reverse the number 854712

Answer: (c)



5. How many letters of the word FAINTS, will their order in the word and that when the letters are arranged in the alphabetical order, remain the same?

(a) Two

(b) One

(c) Three

(d) Nil



Solution:

When the letters are arranged in the alphabetical order, two remains the same.

Answer: (a)



6. In a certain code GARNISH is written as RGAINHS. How will GENIOUS be written in that code?

(a) NEGOISU

(b) NGEOISU

(c) NGESUOI

(d) NEGSUOI



Solution:

So now, GENIOUS be written as;

Answer: (b)



7. How many such pairs of letters are there in the word MISPLACE each of which has as many letters between its two letters in the word as there are between them in the English alphabet?

(a) One

(b) Nil

(c) Two

(d) Three



Solution:

Answer: (c)



8. In a certain code INKER is written as GLLGT and GLIDE is written as EJJFG. How will JINKS be written in that code?

(a) GFOMU

(b) HGMMU

(c) HGOGH

(d) HGOMU



Solution:

As,

And,

Similarly, JINKS be written as;

Answer: (d)



9. If ‘AND’ is written as ‘EQF’ and ‘THE’ as ‘XKG’ then how will ‘COM’ be written?

(a) HRO

(b) GQO

(c) GRO

(d) GRN



Solution:

As,

And,

Similarly, ‘COM’ be written as;

Answer: (c)



10. Four of the following five are alike in a certain way based on the positions of their elements in the English alphabet and hence form a group. Which one does not belong to the group?

(a) UQ

(b) KG

(c) SO

(d) QL



Solution:

QL

Answer: (d)

Read more →

Look at this series: 58, 52, 46, 40, 34, ... What number should come next?

	Look at this series: 58, 52, 46, 40, 34, ... What number should come next?
	A 26                           B 28 C 30                           D 32

Read more →

Math Magic/Tricks

Math Magic/Tricks

Trick 1: Number below 10
Step1: Think of a number below 10.
Step2: Double the number you have thought.
Step3: Add 6 with the getting result.
Step4: Half the answer, that is divide it by 2.
Step5: Take away the number you have thought from the answer, that is, subtract the answer from the number you have thought.

Answer: 3

---

Trick 2: Any Number
Step1: Think of any number.
Step2: Subtract the number you have thought with 1.
Step3: Multiply the result with 3.
Step4: Add 12 with the result.
Step5: Divide the answer by 3.
Step6: Add 5 with the answer.
Step7: Take away the number you have thought from the answer, that is, subtract the answer from the number you have thought.

Answer: 8

---

Trick 3: Any Number
Step1: Think of any number.
Step2: Multiply the number you have thought with 3.
Step3: Add 45 with the result.
Step4: Double the result.
Step5: Divide the answer by 6.
Step6: Take away the number you have thought from the answer, that is, subtract the answer from the number you have thought.

Answer: 15

---

Trick 4: Same 3 Digit Number
Step1: Think of any 3 digit number, but each of the digits must be the same as. Ex: 333, 666.
Step2: Add up the digits.
Step3: Divide the 3 digit number with the digits added up.

Answer: 37

---

Trick 5: 2 Single Digit Numbers
Step1: Think of 2 single digit numbers.
Step2: Take any one of the number among them and double it.
Step3: Add 5 with the result.
Step4: Multiply the result with 5.
Step5: Add the second number to the answer.
Step6: Subtract the answer with 4.
Step7: Subtract the answer again with 21.

Answer: 2 Single Digit Numbers.

---

Trick 6: 1, 2, 4, 5, 7, 8
Step1: Choose a number from 1 to 6.
Step2: Multiply the number with 9.
Step3: Multiply the result with 111.
Step4: Multiply the result by 1001.
Step5: Divide the answer by 7.

Answer: All the above numbers will be present.

---

Trick 7: 1089
Step1: Think of a 3 digit number.
Step2: Arrange the number in descending order.
Step3: Reverse the number and subtract it with the result.
Step4: Remember it and reverse the answer mentally.
Step5: Add it with the result, you have got.

Answer: 1089

---

Trick 8: x7x11x13
Step1: Think of a 3 digit number.
Step2: Multiply it with x7x11x13.

Ex: Number: 456, Answer: 456456

---

Trick 9: x3x7x13x37
Step1: Think of a 2 digit number.
Step2: Multiply it with x3x7x13x37.

Ex: Number: 45, Answer: 454545

---

Trick 10: 9091
Step1:Think of a 5 digit number.
Step2:Multiply it with 11.
Step3:Multiply it with 9091.

Ex: Number: 12345,Answer:1234512345

Read more →

Math

Questions 1: If Logx (1 / 8) = - 3 / 2, then x is equal to A. - 4 B. 4 C. 1 / 4 D. 10  Question 2: 20 % of 2 is equal to A. 20 B. 4 C. 0.4 D. 0.04  Questions 3: If Log 4 (x) = 12, then log 2 (x / 4) is equal to A. 11 B. 48 C. -12 D. 22  Questions 4: The population of a country increased by an average of 2% per year from 2000 to 2003. If the population of this country was 2 000 000 on December 31, 2003, then the population of this country on January 1, 2000, to the nearest thousand would have been A. 1 846 000 B. 1 852 000 C. 1 000 000 D. 1 500 000  Questions 5: f is a quadratic function whose graph is a parabola opening upward and has a vertex on the x-axis. The graph of the new function g defined by g(x) = 2 - f(x - 5) has a range defined by the interval A. [ -5 , + infinity) B. [ 2 , + infinity) C. ( - infinity , 2] D. ( - infinity , 0]  Questions 6: f is a function such that f(x) < 0. The graph of the new function g defined by g(x) = | f(x) | is a reflection of the graph of f A. on the y axis B. on the x axis C. on the line y = x D. on the line y = - x  Questions 7: If the graph of y = f(x) is transformed into the graph of 2y - 6 = - 4 f(x - 3), point (a , b) on the graph of y = f(x) becomes point (A , B) on the graph of 2y - 6 = - 4 f(x - 3) where A and B are given by A. A = a - 3, B = b B. A = a - 3, B = b C. A = a + 3, B = -2 b D. A = a + 3, B = -2 b +3  Questions 8: When a parabola represented by the equation y - 2x 2 = 8 x + 5 is translated 3 units to the left and 2 units up, the new parabola has its vertex at A. (-5 , -1) B. (-5 , -5) C. (-1 , -3) D. (-2 , -3)  Questions 9: The graphs of the two linear equations ax + by = c and bx - ay = c, where a, b and c are all not equal to zero, A. are parallel B. intersect at one point C. intersect at two points D. perpendicular  Questions 10: The graphs of the two equations y = a x 2 + b x + c and y = A x 2 + B x + C, such that a and A have different signs and that the quantities b 2 - 4 a c and B 2 - 4 A C are both negative, A. intersect at two points B. intersect at one point C. do not intersect D. none of the above  Questions 11: For x greater than or equal to zero and less than or equal to 2 pi, sin x and cos x are both decreasing on the intervals A. (0 , pi/2) B. (pi/2 , pi) C. (pi , 3 pi / 2) D. (3 pi / 2 , 2 pi)  Questions 12: The three solutions of the equation f(x) = 0 are -2, 0, and 3. Therefore, the three solutions of the equation f(x - 2) = 0 are A. - 4, -2, and 1 B. -2, 0 and 3 C. 4, 2, and 5 D. 0, 2 and 5  Questions 13: The three solutions of the equation f(x) = 0 are - 4, 8, and 11. Therefore, the three solutions of the equation f(2 x) = 0 are A. - 2, 4, and 11/2 B. - 8, 16 and 22 C. - 4, 8, and 11 D. 2, 19 / 2 and 7 / 2  Questions 14: A school committee consists of 2 teachers and 4 students. The number of different committees that can be formed from 5 teachers and 10 students is A. 10 B. 15 C. 2100 D. 8  Questions 15: Five different books (A, B, C, D and E) are to be arranged on a shelf. Books C and D are to be arranged first and second starting from the right of the shelf. The number of different orders in which books A, B and E may be arranged is A. 5! B. 3! C. 2! D. 3! * 2!  Questions 16: The mean of a data set is equal to 10 and its standard deviation is equal to 1. If we add 5 to each data value, then the mean and standard deviation become A. mean = 15 , standard deviation = 6 B. mean = 10 , standard deviation = 6 C. mean = 15 , standard deviation = 1 D. mean = 10 , standard deviation = 1  Questions 17: The exam scores of all 500 students were recorded and it was determined that these scores were normally distributed. If Jane's score is 0.8 standard deviation above the mean, then how many, to the nearest unit, students scored above Jane? A. 394 B. 250 C. 400 D. 106  Questions 18: If f(x) is an odd function, then | f(x) | is A. an odd function B. an even function C. neither odd nor even D. even and odd  Questions 19: The period of | sin (3x) | is A. 2 pi B. 2 pi / 3 C. pi / 3 D. 3 pi  Questions 20: When a metallic ball bearing is placed inside a cylindrical container, of radius 2 cm, the height of the water, inside the container, increases by 0.6 cm. The radius, to the nearest tenth of a centimeter, of the ball bearing is A. 1 cm B. 1.2 cm C. 2 cm D. 0.6 cm  Questions 21: The period of 2 sin x cos x is A. 4 pi 2 B. 2 pi C. 4 pi D. pi  Questions 22: The probability that an electronic device produced by a company does not function properly is equal to 0.1. If 10 devices are bought, then the probability, to the nearest thousandth, that 7 devices function properly is A. 0.057 B. 0.478 C. 0.001 D. 0  ANSWERS TO ABOVE QUESTIONS 1b, 2c, 3d, 4a, 5c, 6b, 7d, 8a, 9d, 10c 11b, 12d, 13a, 14c, 15b, 16c, 17d, 18b, 19c, 20b 21d, 22a.   1. What is the next prime number after 7? 2. The perimeter of a circle is also known as what? 3. 65 – 43 = ? 4. True or false? A convex shape curves outwards. 5. What does the square root of 144 equal? 6. True or false? Pi can be correctly written as a fraction. 7. What comes after a million, billion and trillion? 8. 52 divided by 4 equals what? 9. What is the bigger number, a googol or a billion? 10. True or false? Opposite angles of a parallelogram are equal. 11. 87 + 56 = ? 12. How many sides does a nonagon have? 13. True or false? -2 is an integer. 14. What is the next number in the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ? 15. 7 x 9 = ? 16. True or false? In an isosceles triangle all sides are unequal. 17. In statistics, the middle value of an ordered set of values is called what? 18. What does 3 squared equal? 19. True or false? -4 is a natural number. 20. 5 to the power of 0 equals what? Math Quiz Answers 1. 11 2. The circumference 3. 22 4. True 5. 12 6. False 7. A quadrillion 8. 13 9. A googol 10. True 11. 143 12. 9 13. True 14. 55 15. 63 16. False (2 sides are equal) 17. The median 18. 9 19. False 20. 1

Read more →

Numerical Problems

Numerical Problems

1. An airplane accelerates down a runway at 3.20 m/s² for 32.8 s until is finally lifts off the ground. Determine the distance traveled before takeoff.
   
   
   
2. A car starts from rest and accelerates uniformly over a time of 5.21 seconds for a distance of 110 m. Determine the acceleration of the car.
   
   
   
3. Upton Chuck is riding the Giant Drop at Great America. If Upton free falls for 2.6 seconds, what will be his final velocity and how far will he fall?
   
   
   
4. A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. Determine the acceleration of the car and the distance traveled.
   
   
   
5. A feather is dropped on the moon from a height of 1.40 meters. The acceleration of gravity on the moon is 1.67 m/s². Determine the time for the feather to fall to the surface of the moon.
   
   
   
6. Rocket-powered sleds are used to test the human response to acceleration. If a rocket-powered sled is accelerated to a speed of 444 m/s in 1.8 seconds, then what is the acceleration and what is the distance that the sled travels?
   
   
   
7. A bike accelerates uniformly from rest to a speed of 7.10 m/s over a distance of 35.4 m. Determine the acceleration of the bike.
   
   
8. An engineer is designing the runway for an airport. Of the planes that will use the airport, the lowest acceleration rate is likely to be 3 m/s². The takeoff speed for this plane will be 65 m/s. Assuming this minimum acceleration, what is the minimum allowed length for the runway?
   
   
   
9. A car traveling at 22.4 m/s skids to a stop in 2.55 s. Determine the skidding distance of the car (assume uniform acceleration).
   
   
   
10. A kangaroo is capable of jumping to a height of 2.62 m. Determine the takeoff speed of the kangaroo.
    
    
    
11. If Michael Jordan has a vertical leap of 1.29 m, then what is his takeoff speed and his hang time (total time to move upwards to the peak and then return to the ground)?
    
    
    
12. A bullet leaves a rifle with a muzzle velocity of 521 m/s. While accelerating through the barrel of the rifle, the bullet moves a distance of 0.840 m. Determine the acceleration of the bullet (assume a uniform acceleration).
    
    
    
13. A baseball is popped straight up into the air and has a hang-time of 6.25 s. Determine the height to which the ball rises before it reaches its peak. (Hint: the time to rise to the peak is one-half the total hang-time.)
    
    
    
14. The observation deck of tall skyscraper 370 m above the street. Determine the time required for a penny to free fall from the deck to the street below.
    
    
    
15. A bullet is moving at a speed of 367 m/s when it embeds into a lump of moist clay. The bullet penetrates for a distance of 0.0621 m. Determine the acceleration of the bullet while moving into the clay. (Assume a uniform acceleration.)
    
    
    
16. A stone is dropped into a deep well and is heard to hit the water 3.41 s after being dropped. Determine the depth of the well.
    
    
    
17. It was once recorded that a Jaguar left skid marks that were 290 m in length. Assuming that the Jaguar skidded to a stop with a constant acceleration of -3.90 m/s², determine the speed of the Jaguar before it began to skid.
    
    
    
18. A plane has a takeoff speed of 88.3 m/s and requires 1365 m to reach that speed. Determine the acceleration of the plane and the time required to reach this speed.
    
    
    
19. A dragster accelerates to a speed of 112 m/s over a distance of 398 m. Determine the acceleration (assume uniform) of the dragster.
    
    
20. With what speed in miles/hr (1 m/s = 2.23 mi/hr) must an object be thrown to reach a height of 91.5 m (equivalent to one football field)? Assume negligible air resistance.  

 Solutions:

1. Given: a = +3.2 m/s2 t = 32.8 s vi = 0 m/s

   Find: d = ??

   d = v_i*t + 0.5*a*t² d = (0 m/s)*(32.8 s)+ 0.5*(3.20 m/s²)*(32.8 s)²
   d = 1720 m

2. Given: d = 110 m t = 5.21 s vi = 0 m/s

   Find: a = ??

   d = v_i*t + 0.5*a*t² 110 m = (0 m/s)*(5.21 s)+ 0.5*(a)*(5.21 s)²
   110 m = (13.57 s²)*a
   a = (110 m)/(13.57 s²)
   a = 8.10 m/ s²

3. Given: a = -9.8 m t = 2.6 s vi = 0 m/s

   Find: d = ?? vf = ??

   d = v_i*t + 0.5*a*t² d = (0 m/s)*(2.6 s)+ 0.5*(-9.8 m/s²)*(2.6 s)²
   d = -33 m (- indicates direction)
   v_f = v_i + a*t
   v_f = 0 + (-9.8 m/s²)*(2.6 s)
   v_f = -25.5 m/s (- indicates direction)

4. Given: vi = 18.5 m/s vf = 46.1 m/s t = 2.47 s

   Find: d = ?? a = ??

   a = (Delta v)/t a = (46.1 m/s - 18.5 m/s)/(2.47 s)
   a = 11.2 m/s²
   d = v_i*t + 0.5*a*t²
   d = (18.5 m/s)*(2.47 s)+ 0.5*(11.2 m/s²)*(2.47 s)²
   d = 45.7 m + 34.1 m
   d = 79.8 m
   (Note: the d can also be calculated using the equation v_f² = v_i² + 2*a*d)

5. Given: vi = 0 m/s d = -1.40 m a = -1.67 m/s2

   Find: t = ??

   d = v_i*t + 0.5*a*t² -1.40 m = (0 m/s)*(t)+ 0.5*(-1.67 m/s²)*(t)²
   -1.40 m = 0+ (-0.835 m/s²)*(t)²
   (-1.40 m)/(-0.835 m/s²) = t²
   1.68 s² = t²
   t = 1.29 s

6. Given: vi = 0 m/s vf = 44 m/s t = 1.80 s

   Find: a = ?? d = ??

   a = (Delta v)/t a = (444 m/s - 0 m/s)/(1.80 s)
   a = 247 m/s²
   d = v_i*t + 0.5*a*t²
   d = (0 m/s)*(1.80 s)+ 0.5*(247 m/s²)*(1.80 s)²
   d = 0 m + 400 m
   d = 400 m
   (Note: the d can also be calculated using the equation v_f² = v_i² + 2*a*d)

7. Given: vi = 0 m/s vf = 7.10 m/s d = 35.4      m

   Find: a = ??

   v_f² = v_i² + 2*a*d (7.10 m/s)² = (0 m/s)² + 2*(a)*(35.4 m)
   50.4 m²/s² = (0 m/s)² + (70.8 m)*a
   (50.4 m²/s²)/(70.8 m) = a
   a = 0.712 m/s²

8. Given: vi = 0 m/s vf = 65 m/s a = 3 m/s2

   Find: d = ??

   v_f² = v_i² + 2*a*d (65 m/s)² = (0 m/s)² + 2*(3 m/s²)*d
   4225 m²/s² = (0 m/s)² + (6 m/s²)*d
   (4225 m²/s²)/(6 m/s²) = d
   d = 704 m

9. Given: vi = 22.4 m/s vf = 0 m/s t = 2.55      s

   Find: d = ??

   d = (v_i + v_f)/2 *t d = (22.4 m/s + 0 m/s)/2 *2.55 s
   d = (11.2 m/s)*2.55 s
   d = 28.6 m

10. Given: a = -9.8 m/s2 vf = 0 m/s d = 2.62      m

    Find: vi = ??

    v_f² = v_i² + 2*a*d (0 m/s)² = v_i² + 2*(-9.8 m/s²)*(2.62 m)
    0 m²/s² = v_i² - 51.35 m²/s²
    51.35 m²/s² = v_i²
    v_i = 7.17 m/s

11. Given: a = -9.8 m/s2 vf = 0 m/s d = 1.29      m

    Find: vi = ?? t = ??

    v_f² = v_i² + 2*a*d (0 m/s)² = v_i² + 2*(-9.8 m/s²)*(1.29 m)
    0 m²/s² = v_i² - 25.28 m²/s²
    25.28 m²/s² = v_i²
    v_i = 5.03 m/s
    To find hang time, find the time to the peak and then double it.
    v_f = v_i + a*t
    0 m/s = 5.03 m/s + (-9.8 m/s²)*t_up
    -5.03 m/s = (-9.8 m/s²)*t_up
    (-5.03 m/s)/(-9.8 m/s²) = t_up
    t_up = 0.513 s
    hang time = 1.03 s

12. Given: vi = 0 m/s vf = 521 m/s d = 0.840 m

    Find: a = ??

    v_f² = v_i² + 2*a*d (521 m/s)² = (0 m/s)² + 2*(a)*(0.840 m)
    271441 m²/s² = (0 m/s)² + (1.68 m)*a
    (271441 m²/s²)/(1.68 m) = a
    a = 1.62*10⁵ m /s²

13. Given: a = -9.8 m/s2 vf = 0 m/s t = 3.13      s

    Find: d = ??

    1. (NOTE: the time required to move to the peak of the trajectory is one-half the total hang time.)
    First use: v_f = v_i + a*t 0 m/s = v_i + (-9.8 m/s²)*(3.13 s)
    0 m/s = v_i - 30.6 m/s
    v_i = 30.6 m/s
    Now use: v_f² = v_i² + 2*a*d
    (0 m/s)² = (30.6 m/s)² + 2*(-9.8 m/s²)*(d)
    0 m²/s² = (938 m/s) + (-19.6 m/s²)*d
    -938 m/s = (-19.6 m/s²)*d
    (-938 m/s)/(-19.6 m/s²) = d
    d = 47.9 m

14. Given: vi = 0 m/s d = -370 m a = -9.8 m/s2

    Find: t = ??

    d = v_i*t + 0.5*a*t² -370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s²)*(t)²
    -370 m = 0+ (-4.9 m/s²)*(t)²
    (-370 m)/(-4.9 m/s²) = t²
    75.5 s² = t²
    t = 8.69 s

15. Given: vi = 367 m/s vf = 0 m/s d = 0.0621 m

    Find: a = ??

    v_f² = v_i² + 2*a*d (0 m/s)² = (367 m/s)² + 2*(a)*(0.0621 m)
    0 m²/s² = (134689 m²/s²) + (0.1242 m)*a
    -134689 m²/s² = (0.1242 m)*a
    (-134689 m²/s²)/(0.1242 m) = a
    a = -1.08*10⁶ m /s²
    (The - sign indicates that the bullet slowed down.)

16. Given: a = -9.8 m/s2 t = 3.41 s vi = 0 m/s

    Find: d = ??

    d = v_i*t + 0.5*a*t² d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s²)*(3.41 s)²
    d = 0 m+ 0.5*(-9.8 m/s²)*(11.63 s²)
    d = -57.0 m
    (NOTE: the - sign indicates direction)

17. Given: a = -3.90 m/s2 vf = 0 m/s d = 290      m

    Find: vi = ??

    v_f² = v_i² + 2*a*d (0 m/s)² = v_i² + 2*(-3.90 m/s²)*(290 m)
    0 m²/s² = v_i² - 2262 m²/s²
    2262 m²/s² = v_i²
    v_i = 47.6 m /s

18. Given: vi = 0 m/s vf = 88.3 m/s d = 1365      m

    Find: a = ?? t = ??

    v_f² = v_i² + 2*a*d (88.3 m/s)² = (0 m/s)² + 2*(a)*(1365 m)
    7797 m²/s² = (0 m²/s²) + (2730 m)*a
    7797 m²/s² = (2730 m)*a
    (7797 m²/s²)/(2730 m) = a
    a = 2.86 m/s²
    v_f = v_i + a*t
    88.3 m/s = 0 m/s + (2.86 m/s²)*t
    (88.3 m/s)/(2.86 m/s²) = t
    t = 30. 8 s

19. Given: vi = 0 m/s vf = 112m/s d = 398 m

    Find: a = ??

    v_f² = v_i² + 2*a*d (112 m/s)² = (0 m/s)² + 2*(a)*(398 m)
    12544 m²/s² = 0 m²/s² + (796 m)*a
    12544 m²/s² = (796 m)*a
    (12544 m²/s²)/(796 m) = a
    a = 15.8 m/s²

20. Given: a = -9.8 m/s2 vf = 0 m/s d = 91.5      m

    Find: vi = ?? t = ??

    First, find speed in units of m/s: v_f² = v_i² + 2*a*d
    (0 m/s)² = v_i² + 2*(-9.8 m/s²)*(91.5 m)
    0 m²/s² = v_i² - 1793 m²/s²
    1793 m²/s² = v_i²
    v_i = 42.3 m/s
    Now convert from m/s to mi/hr:
    v_i = 42.3 m/s * (2.23 mi/hr)/(1 m/s)
    v_i = 94.4 mi/hr

Read more →